Задача
а) На каждой стороне десятиугольника (не обязательно выпуклого) как на диаметре построили окружность. Может ли оказаться, что все эти окружности имеют общую точку, не совпадающую ни с одной вершиной десятиугольника?
б) Решите ту же задачу для одиннадцатиугольника.
Решение
Наличие общей точки у всех построенных окружностей равносильно существованию точки, из которой каждая сторона многоугольника видна под прямым углом. а) См. рис.
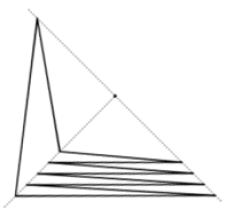
OA1 || OA3 || ... || OA11 || OA2. Противоречие.
Ответ
а) Может; б) не может.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет