Задача
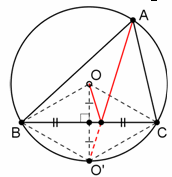
Из вершины A остроугольного треугольника ABC по биссектрисе угла A выпустили бильярдный шарик, который отразился от стороны BC по закону "угол падения равен углу отражения" и дальше катился по прямой, уже ни от чего не отражаясь. Докажите, что если ∠A = 60°, то траектория шарика проходит через центр описанной окружности треугольника ABC.
Решение
Отразим относительно BC центр O описанной окружности Ω треугольника ABC. Получим точку O'. Так как
∠BO'C = ∠BOC = 2∠A = 120° = 180° – ∠A, то O' лежит на Ω. Так как O лежит на серединном перпендикуляре к BC, то O' – середина дуги BC. Значит, биссектриса угла A проходит через O'. Это и значит, что после отражения шарик пройдёт через точку O.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь