Задача
В турнире по волейболу каждая команда встречалась с каждой по одному разу. Каждая встреча состояла из нескольких партий – до трёх побед одной из команд. Если встреча заканчивалась со счётом 3 : 0 или 3 : 1, то выигравшая команда получала 3 очка, а проигравшая – 0. Если же счёт партий был
3 : 2, то победитель получал 2 очка, а побеждённый – 1 очко. По итогам турнира оказалось, что команда "Хитрецы" набрала больше всех очков, а команда "Простаки" – меньше всех. Но "Хитрецы" выиграли меньше встреч, чем проиграли, а у "Простаков" наоборот, победных встреч оказалось больше, чем проигранных. При каком наименьшем количестве команд такое возможно?
Решение
Оценка. Если команд не больше трёх, то "Простаки" выиграли все встречи, значит, и очков у них больше всех. Противоречие.
Если команд четыре или пять, то каждая команда проведёт три или четыре встречи. Значит, "Хитрецы" выиграли не более одной встречи и набрали максимум 5 = 3 + 1 + 1 или 6 = 3 + 1 + 1 + 1 очков соответственно. "Простаки" же выиграли не менее двух встреч при четырёх участниках и не менее трёх встреч при пяти участниках, то есть набрали минимум 4 = 2 + 2 + 0 или 6 = 2 + 2 + 2 + 0 очков соответственно. Учитывая, что "Хитрецы" должны набрать хотя бы на 2 очка больше, чем "Простаки", получаем противоречие.
Следовательно, команд не меньше шести.
Пример. См. таблицу.
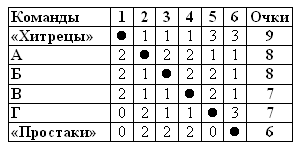
Ответ
При шести командах.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь