Задача
Неправдоподобная легенда гласит, что однажды Стирлинг размышлял над числами Стирлинга второго рода и в задумчивости бросал на стол 10 правильных игральных костей. После очередного броска он вдруг заметил, что в выпавшей комбинации очков присутствуют все числа от 1 до 6. Тут же Стирлинг задумался, а какова же вероятность такого события? Какова вероятность, что при бросании 10 костей каждое число очков от 1 до 6 выпадет хотя бы на одной кости?
Решение
Найдём вероятность события A "в выпавшей комбинации какого-то числа нет". Обозначим Ak событие "нет числа k". Тогда
A = A1 ∪ A2 ∪ A3 ∪ A4 ∪ A5 ∪ A6.
С помощью формулы включения-исключения получаем:
P(A) = P(A1) + P(A2) + ... + P(A6) – P(A1∩A2) – P(A1∩A3) – ... – P(A5∩A6) + P(A1∩A2∩A3) + P(A1∩A2∩A4) + ... + P(A4∩A5∩A6) – ... – P(A1∩A2∩A3∩A4∩A5∩A6).
Все вероятности P(Ak) равны (5/6)10, а всего их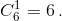 
Вероятности попарных пересечений равны (4/6)10, а всего их 
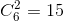и т.д. Значит,
P(A) = 6·(5/6)10 – 15·(4/6)10 + 20·(3/6)10 – 15·(2/6)10 + 6·(1/6)10.
Следовательно, вероятность того, что каждое число встретится хотя бы раз, равна 1 – P(A).
Ответ
1 – 6·(5/6)10 + 15·(4/6)10 – 20·(3/6)10 + 15·(2/6)10 – 6·(1/6)10 ≈ 0,272.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь