Задача
В турнире участвуют 100 борцов, все разной силы. В любом поединке двух борцов всегда побеждает тот, кто сильнее. В первом туре борцы разбились на случайные пары и провели поединки. Для второго тура борцы ещё раз разбиваются на случайные пары соперников (может случиться, что какие-то пары повторятся). Приз получает тот, кто выиграет оба поединка. Найдите: а) наименьшее возможное число призёров турнира; б) математическое ожидание числа призеров турнира.
Решение
а) См. задачу 164440. б) Пронумеруем борцов от самого слабого №1 до самого сильного №100. Пусть Ik – индикатор события "k-й борец выиграл оба поединка". Вероятность победить соперника в каждом поединке для k-го борца равна вероятности того, что его соперником оказался один из тех k – 1 борцов, что слабее. Значит, вероятность победы равна k–1/99. Вероятность победить оба раза равна (k–1/99)², поэтому EIk = (k–1/99)².
Общее количество призёров X равно сумме всех индикаторов, значит,
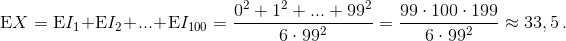
Ответ
а) 1; б) ≈33,5.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь