Задача
На берёзе сидели белые и чёрные вороны – всего их было 50. Белые точно были, а чёрных было не меньше, чем белых. На дубе тоже сидели белые и чёрные вороны, и было их всего 50. На дубе чёрных тоже было не меньше, чем белых или столько же, а может быть, даже на одну меньше. Одна случайная ворона перелетела с берёзы на дуб, а через некоторое время другая (может быть, та же самая) случайная ворона перелетела с дуба на берёзу. Что более вероятно: что количество белых ворон на берёзе стало таким же, как было сначала, или что оно изменилось?
Решение
Пусть на берёзе было a белых и b чёрных ворон, а на дубе – c белых и d чёрных. Вероятности перелётов чёрных и белых ворон с берёзы на дуб и обратно изобразим с помощью дерева. Точка S – начало, событие B – перелёт чёрной вороны, событие W – перелёт белой.
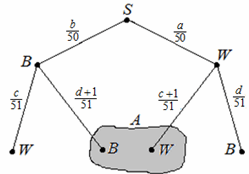
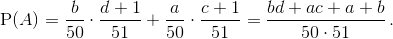Вероятность противоположного события "Численность изменилась" получается сложением вероятностей вдоль цепочекSBWиSWB: 
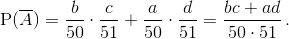Имеем 50·51(P(A) – P(A)) = (b – a)(d – c) +a + b ≥ a – b + a + b= 2a> 0 (по условию b – a≥ 0, d – c≥ –1).
Ответ
Что количество белых ворон станет прежним.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь