Задача
Две окружности пересекаются в точках А и В. Через точку В проведена прямая, пересекающая окружности в точках М и N так, что АВ – биссектриса треугольника МАN. Докажите, что отношение отрезков ВМ и BN равно отношению радиусов окружностей.
Решение
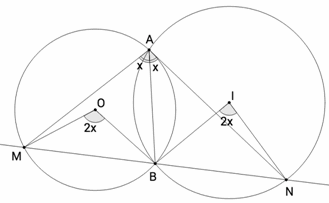
Пусть О и I – центры данных окружностей, а R и r – их радиусы (см. рис.).
Так как ∠MOB = 2∠MАB = 2∠NАB = ∠NIB, то равнобедренные треугольники MOB и NIB подобны. Значит, BM : BN = OM : IN = R : r.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет