Назад
Задача 165986 • Сложность: 2 • 9-11 класс
Задача

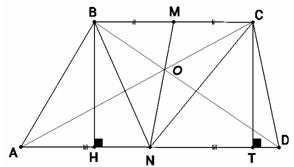
Диагонали четырёхугольника АВСD пересекаются в точке О, М и N – середины сторон ВС и AD соответственно. Отрезок MN делит площадь четырёхугольника пополам. Найдите отношение  ОМ : ОN,  если  AD = 2BC.

Разделы:
Планиметрия
Источники:
Московская математическая регата Олимпиады и турниры 2016/2017
Количество версий:
4
Решение

  NM – медиана треугольника BNC (см. рис.), поэтому  SBMN = SСMN.

  Из условия теперь следует, что  SABN = SDСN.  Кроме того, у треугольниковABNиDСNравны стороныANиDN, поэтому их высотыBHиCTтакже равны. Следовательно,  AD || BC,  то естьABCD– трапеция.   Значит, точкаОлежит на отрезкеMN, а треугольникиAODиCOBподобны с коэффициентом  AD/BC= 2.  Так какONиOM– соответствующие медианы этих треугольников, то и  ОМ:ОN= 1 : 2.
Ответ

1 : 2.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет