Задача
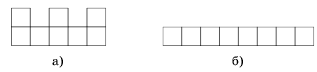
Можно ли так расставить цифры 1, 2, ..., 8 в клетках а) буквы Ш; б) полоски (см. рис.), чтобы при любом разрезании фигуры на две части сумма всех цифр в одной из частей делилась на сумму всех цифр в другой? (Резать можно только по границам клеток. В каждой клетке должна стоять одна цифра, каждую цифру можно использовать только один раз.)
Решение
Пусть сумма чисел в одной из частей равна m, в другой n и n делится на m. Тогда и m + n делится на m, а это сумма всех чисел, она равна
1 + 2 + ... 8 = 36. Значит, меньшая из сумм частей является делителем числа 36.
Верно и обратное: если 36 делится на m, то и 36 – m делится на m. а) Для фигуры, заполненной как на рисунке, при разрезании на две части получаются такие меньшие суммы: 2, 2 + 7 = 9, 2 + 7 + 3 = 12, 1,
6 + 8 + 4 = 18, 8 + 4 = 12, 4. Все они являются делителями числа 36.
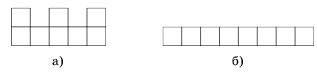
Предположим, что расставить числа в полоске требуемым образом удалось. Выпишем сумму чисел в первой клетке, первых двух клетках, первых трёх клетках и т. д. У нас получится возрастающая последовательность из восьми чисел, первое из которых не больше 8, а последнее равно 36. При этом соседние члены этой последовательности различаются не больше чем на 8.
Если в этой последовательности есть число 18, то предыдущее число должно быть не менее 18 − 8 = 10. Единственное число между 10 и 18 в последовательности – это 12. Следовать за 18 может число не более 18 + 8 = 26, подходит только 24. Но тогда в двух разных клетках должно стоять число 6 = 18 − 12 = 24 − 18. Следовательно, числа 18 в этой последовательности нет.
Посмотрим на то место, где после числа, меньшего 18, идёт число, большее 18. Разность этих чисел должна быть равна как минимум 24 − 12 = 12. Но они должны отличаться на число, не большее 8. Противоречие.
Ответ
а) Можно; б) нельзя.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь