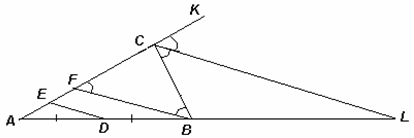
Пусть CL – биссектриса внешнего угла С, D – середина АВ, K – точка на продолжении стороны АС за точку С (см. рис.).   Первый способ. Через вершину В проведём прямую, параллельную CL, F – точка её пересечения с прямой АС. Тогда треугольник BCF – равнобедренный. Действительно,  ∠СFB = ∠KCL = ∠BCL = ∠СBF,  значит,  CF = CB.

  Так как  АС > BC,  то F лежит на отрезке АС. Кроме того, так как  DE || BF  и D – середина АВ, то  AE = EF.

  Таким образом,  AE = ½ (AC – CF) = ½ (AC – BC) = 1,5.

  Второй способ. По теореме о биссектрисе внешнего угла треугольника  LA : LB = CA : CB = 8 : 5.  По теореме Фалеса  AE : AC = AD : AL = 3 : 16.

  Значит,  AE = ³/₁₆ AC = 1,5.

1,5.