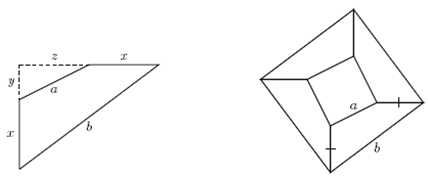
Пусть  b > a.   Первый способ. Обозначим длину двух равных сторон через x. Продолжим их до пересечения и обозначим длины двух получившихся коротких отрезков через y и z (рис. слева).   ПлощадьSисходного четырёхугольника есть разность площадей двух прямоугольных треугольников: с катетами  x + y  и  x + z  и с катетамиyиz. Поэтому  2S= (x + y)(x + z) –yz = x² +xy + xz.   По теореме Пифагора  y² +z² =a²,  (x + y)² + (x + z)² =b².  Поэтому  b² –a² = 2x² + 2xy+ 2xz= 4S.

 Второй способ. Из четырёх таких многоугольников можно сложить квадрат со сторонойbиз которого вырезан квадрат со сторонойa(рис. справа). Поэтому площадь одного многоугольника равна  ¼ (b² –a²).

¼ |b² – a²|.