Пусть  ∠ACD = α,  ∠BCD = β,  ∠BCA = γ,  DA = a,  DB = b.  По условию  CD = a + b,  а доказать требуется, что  α + β + γ = 90°.   Первый способ. Пусть  CA = m,  CB = n  (рис. слева).

  Сначала докажем, что углы  α + β  и γ – острые. Действительно, в прямоугольных треугольниках ACD и ВCD катеты AD и BD – наименьшие, значит,

α < 45°  и  β < 45°.  Следовательно,  γ < α + β < 90°.  Теперь достаточно проверить, что  sin (α + β) = cos γ.

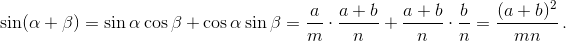
  Поскольку плоскости ACD и BCD перпендикулярны, то по теореме косинусов для трёхгранного угла (см. задачу 161247)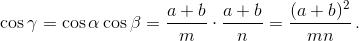

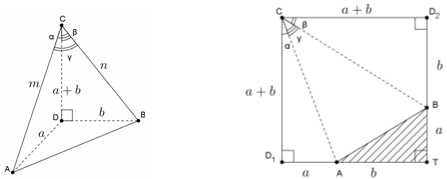
  Рассмотрим квадрат СD₁TD₂ со стороной  a + b  и отложим на его сторонах TD₁ и TD₂ отрезки  TA = b  и  TB = a  соответственно (рис. справа). Тогда пятиугольник ABD₂CD₁ является развёрткой боковой поверхности данной пирамиды, а треугольник ATB равен треугольнику ADB её основания. Таким образом, выполняются все условия задачи, значит,  α + β + γ = 90°.

Ответ задачи отсутствует