Задача
Правильный пятиугольник и правильный двадцатиугольник вписаны в одну и ту же окружность.
Что больше: сумма квадратов длин всех сторон пятиугольника или сумма квадратов длин всех сторон двадцатиугольника?
Решение
Заметим, что в правильном двадцатиугольнике вершины, взятые через одну, образуют правильный десятиугольник, а вершины этого десятиугольника, взятые через одну, образуют правильный пятиугольник. Достаточно сравнить две величины: 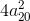 и
и 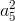 , где a20 и a5 – длины сторон правильных двадцатиугольника и пятиугольника соответственно. Докажем, что
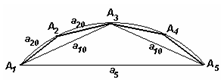
, где a20 и a5 – длины сторон правильных двадцатиугольника и пятиугольника соответственно. Докажем, что 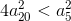 , то есть сумма квадратов сторон пятиугольника больше. Первый способ. Рассмотрим соответствующий фрагмент и введём обозначения вершин так, как показано на рисунке. Заметим, что при n > 4 угол правильного n-угольника – тупой. Рассмотрим треугольник А1А2А3 с тупым углом А2. По следствию из теоремы косинусов
, то есть сумма квадратов сторон пятиугольника больше. Первый способ. Рассмотрим соответствующий фрагмент и введём обозначения вершин так, как показано на рисунке. Заметим, что при n > 4 угол правильного n-угольника – тупой. Рассмотрим треугольник А1А2А3 с тупым углом А2. По следствию из теоремы косинусов 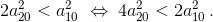 Аналогично из треугольника А1А3А5 получим, что
Аналогично из треугольника А1А3А5 получим, что 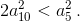 Таким образом,
Таким образом, 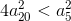 .
.
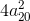 Следовательно,
Следовательно, 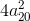
Ответ
Сумма квадратов длин сторон правильного пятиугольника.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь