Задача
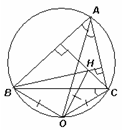
Высоты неравнобедренного остроугольного треугольника ABC пересекаются в точке H. O – центр описанной окружности треугольника BHC. Центр I вписанной окружности треугольника ABC лежит на отрезке OA. Найдите угол A.
Решение
Из условия следует, что точка O лежит на пересечении биссектрисы угла A и серединного перпендикуляра к стороне BC. Так как эти прямые пересекаются на описанной окружности треугольника ABC, то O лежит на этой окружности и является серединой дуги ВС. Кроме того,
∠ВНС = 180° – ∠А, так как Н – ортоцентр треугольника АВС.
BOC – центральный угол, опирающийся на дугу BHC описанной окружности треугольника BHC. Следовательно,
∠ВНС = 180° – ½ ∠BOC = 180° – ½ (180° – ∠А) = 90° + ½ ∠А.
Значит, ∠90° + ½ ∠А = 180° – ∠А, откуда ∠А = 60°.
Ответ
60°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь