Задача
В остроугольном треугольнике ABC проведены высоты AD и CE. Точки M и N – основания перпендикуляров, опущенных на прямую DE из точек A и C соответственно. Докажите, что ME = DN.
Решение
Заметим, что точки D и E лежат на окружности с диаметром AC. Далее можно рассуждать по-разному. Первый способ. По свойству вписанного четырёхугольника ∠NDC = ∠А = α, ∠MEA = ∠С = γ (рис. слева). Используя прямоугольные треугольники АМЕ и АЕС, получим: МЕ = АЕ cos γ = AC cos α cos γ. Аналогично DN = AC cos γ cos α = ME.
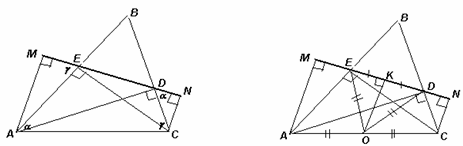
ЕК = КD (рис. справа). Прямые АМ, ОК и CN перпендикулярны прямой ED, поэтому параллельны друг другу. Значит, ОK – средняя линия трапеции AМNC. Следовательно, ME = МК – ЕК = КN – КD = DN.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь