Задача
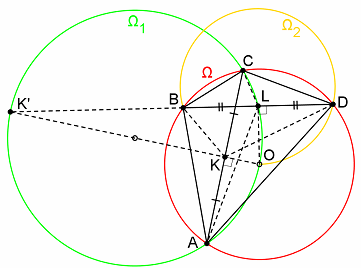
Четырёхугольник ABCD вписан в окружность Ω с центром O, причём O не лежит на диагоналях четырёхугольника. Описанная окружность Ω1 треугольника AOC проходит через середину диагонали BD. Докажите, что описанная окружность Ω2 треугольника BOD проходит через середину диагонали AC.
Решение
Пусть K и L – середины AC и BD соответственно. Отрезки OK и OL перпендикулярны соответственно хордам AC и BD окружности Ω. Пусть K' – точка, диаметрально противоположная точке O на Ω1. Поскольку L лежит на Ω1, то угол OLK' прямой. Значит, прямая BD проходит через K'. Далее можно рассуждать по-разному. Первый способ. Можно считать, что углы A и D острые (см. рис.). Углы ALB и BLC равны как опирающиеся на равные дуги AK' и CK' окружности Ω1. Поэтому ∠BLC = ½ ∠ALC = ½ ∠AOC = ∠ADC. Значит, треугольники ACD и BCL подобны по двум углам. Отсюда AC : AD = BC : BL, то есть
BC·AD = BL·AC = ½ BD·AC. По теореме Птолемея DC·AB = BC·AD = ½ BD·AC = KC·BD.
Из равенства DC·AB = KC·BD следует подобие треугольников CKD и BAD (по двум сторонам и углу между ними). Следовательно, ∠CKD = ∠BAD. Аналогично из равенства BC·AD = KC·BD получаем, что равны углы CKB и BAD. Поэтому ∠BKD = 2∠BAD = ∠BOD, то есть точка K лежит на окружности Ω2.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь