Задача
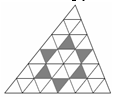
Произвольный треугольник разрезали на равные треугольники прямыми, параллельными сторонам (как показано на рисунке).
Докажите, что ортоцентры шести закрашенных треугольников лежат на одной окружности.
Решение
Решение 1:Пусть H – ортоцентр одного из закрашенных треугольников. Присоединив к нему три соседних белых треугольника, получим двойной треугольник. Понятно, что H является в этом двойном треугольнике центром описанной окружности. Проделав такие действия для всех закрашенных треугольников, получим шесть равных двойных треугольников с общей вершиной T. Поэтому ортоцентры всех закрашенных треугольников лежат на окружности с центром T радиуса TH.
Решение 2:Рассмотрим два закрашенных треугольника с общей вершиной A. Они симметричны относительно A. Их высоты, выходящие из A, перпендикулярны TA, где T – центр большого треугольника. Значит, их ортоцентры симметричны относительно TA. Поэтому расстояние от T до этих ортоцентров одно и то же. Поскольку это верно для любой пары соседних закрашенных треугольников, то ортоцентры всех этих треугольников равноудалены от T.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь