Задачи и олимпиады по математике

Задача

Криволинейный многоугольник – это многоугольник, стороны которого – дуги окружностей. Существуют ли такой криволинейный многоугольник P и такая точка A на его границе, что каждая прямая, проходящая через точку A, делит периметр многоугольника P на два куска равной длины?

Решение

Один из примеров состоит из полуокружности радиуса 2 и двух полуокружностей радиуса 1 (рис. слева).

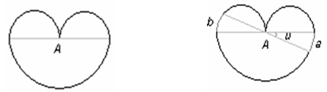
Ясно, что "горизонтальный" отрезок делит периметр пополам. Проведём любую другую прямую через точкуAпод некоторым угломu(измеренным в радианах) к отрезку (рис. справа). От нижней части отнялась дуга a = u·2 (здесь уголuцентральный) и прибавилась равная по длине дуга b= 2u (здесь уголuвписанный).

Ответ

Существуют.

Задача

Решение

Ответ

Подтверждение удаления