Задача
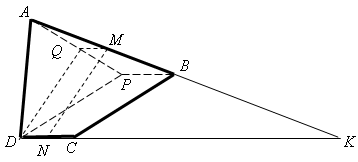
Продолжения сторон AB и CD выпуклого четырёхугольника ABCD пересекаются в точке K. Известно, что AD = BC. Пусть M и N – середины сторон AB и CD. Докажите, что треугольник MNK тупоугольный.
Решение
Пусть B и C ближе к точке K, чем A и D соответственно. Первый способ. Поскольку ∠MBC + ∠NCB > 180° > ∠MAD + ∠NDA, то ∠MBC > ∠MAD или ∠NCB > ∠NDA. Пусть ∠NCB > ∠NDA. В треугольниках NCB и NDA равны две пары сторон. Поэтому NB > NA (например, по теореме косинусов). По тем же соображениям, из сравнения треугольников NMB и NMA имеем ∠NMB > ∠NMA. Значит, угол NMB тупой. Второй способ. ∠KCB + ∠KBC = ∠KDA + ∠KAD. Заметим, однако, что AD и BC непараллельны. Поэтому либо ∠KCB < ∠KDA, либо
∠KBC < ∠KAD. Будем считать, что выполнено первое неравенство.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь