Задача
Билет на электричку стоит 50 рублей, а штраф за безбилетный проезд – 450 рублей. Если безбилетник (заяц) попадается контролёру, то оплачивает и штраф, и стоимость билета. Известно, что контролёр встречается в среднем один раз на 10 поездок. Заяц ознакомился с основами теории вероятностей и решил придерживаться стратегии, которая делает математическое ожидание расходов наименьшим возможным. Как ему поступать: покупать билет каждый раз, не покупать никогда или бросать монетку – покупать билет или нет?
Решение
Пусть вероятность покупки билета p, а вероятность появления контролера q. Случайная величина X "Расходы на поездку" имеет распределение 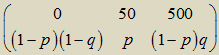 .
.
Математическое ожидание расходов EX = 50p + 500(1 – p)q = 500q – 50p(10q – 1).
По условию q = 0,1. Следовательно, EX = 50, то есть не зависит от p. Возникает "равновесие" – средний расход на поездку не зависит от частоты или вероятности покупки билета.
Ответ
Все равно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь