Задача
Две хоккейные команды одинаковой силы договорились, что будут играть до тех пор, пока суммарный счёт не достигнет 10.
Найдите математическое ожидание числа моментов, когда наступала ничья.
Решение
Если 2n – максимальный суммарный счёт, то игру можно рассматривать как случайное блуждание длины 2n: на каждом шаге разрыв в счете либо увеличивается на единицу, либо уменьшается на единицу.
Пусть I2k – индикатор ничьей на 2k-м шаге: 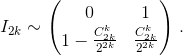
Случайная величина X "число моментов, когда наступала ничья" равна сумме всех индикаторов. Начало игры не будем считать "наступлением ничьей". Следовательно, X = I2 + I4 + ... + I2n, а 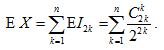
При n = 5 получаем EX = 2/4 + 6/16 + 20/64 + 70/256 + 252/2048 ≈ 1,707.
Ответ
≈ 1,707.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь