Задача
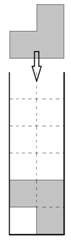
Высокий прямоугольник ширины 2 открыт сверху, и в него падают в случайной ориентации Г-тримино (см. рисунок).
а) Упало k тримино. Найдите математическое ожидание высоты получившегося многоугольника.
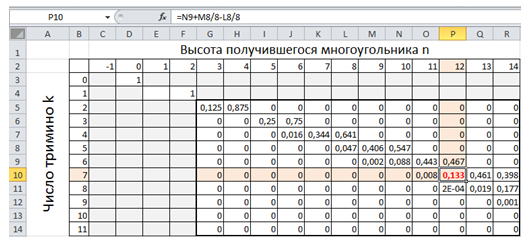
б) Упало 7 тримино. Найдите вероятность того, что сложенная из тримино фигура будет иметь высоту 12.
Решение
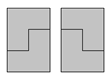
а) Случайную величину "высота получившегося многоугольника" обозначим X. Очевидно, X = 2k – (I2 + I3 + ... + Ik), где Ij – индикатор события "тримино с номерами j и j – 1 образовали блок высоты 3". Это может быть только в двух случаях, показанных на рисунке. Вероятность такого равна ⅛. Таким образом, EIj = ⅛. Поэтому EX = 2k – ⅛ (k – 1) = 15k+1/8.
Ответ
а) 15k+1/8; б) ≈ 0,133.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет