Задача
В выпуклом многоугольнике, в котором нечётное число вершин, равное 2n + 1, выбирают независимо друг от друга две случайные диагонали.
Найдите вероятность того, что эти диагонали пересекаются внутри многоугольника.
Решение
Всего в (2n+1)-угольнике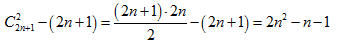 
диагоналей, и, следовательно, пар диагоналей всего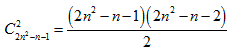 
Две пересекающиеся диагонали однозначно определяются выбором четырёх вершин, значит, способов выбрать две пересекающиеся диагонали 
Диагонали выбираются случайным образом, поэтому все комбинации равновозможны. Значит, вероятность того, что две случайные диагонали пересекаются, равна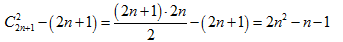 
Ответ
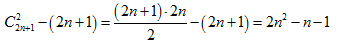
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет