Задача
На заводе имени матроса Железняка изготавливают прямоугольники длиной 2 м и шириной 1 м. Длину отмеряет рабочий Иванов, а ширину, независимо от Иванова, отмеряет рабочий Петров. Средняя ошибка у обоих нулевая, но Иванов допускает стандартную ошибку измерения (стандартное отклонение длины) 3 мм, а Петров допускает стандартную ошибку 2 мм.
а) Найдите математическое ожидание площади получившегося прямоугольника.
б) Найдите стандартное отклонение площади получившегося прямоугольника в квадратных сантиметрах.
Решение
а) Пусть X – ширина, а Y – длина вырезанного прямоугольника в метрах. По условию EX = 2, EY = 1. Поскольку измерения независимы,
E(XY) = EX·EY = 2 (м²). б) Из условия следует, что DX = 0,003² = 9·10–6 и DY = 4·10–6. D(XY) = E(XY)² – E²(XY) = EX²·EY² – 4.
Из равенства DX = EX² – E²X выразим EX² и подставим в полученное выражение. Аналогично поступим с EY²:
D(XY) = (DX + E²X)(DY + E²Y) – 4 = (4·10–6 + 1)(9·10–6 + 4) – 4 = 36·10–12 + 25·10–6.
По сравнению со вторым слагаемым первое настолько мало, что его можно отбросить. Получаем: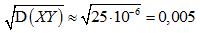 
(м²), что дает 50 см².
Ответ
а) 2 м²; б) ≈50 см².
Чтобы оставлять комментарии, войдите или зарегистрируйтесь