Задача
В выпуклом шестиугольнике независимо друг от друга выбраны две случайные диагонали.
Найдите вероятность того, что эти диагонали пересекаются внутри шестиугольника (внутри – то есть не в вершине).
Решение
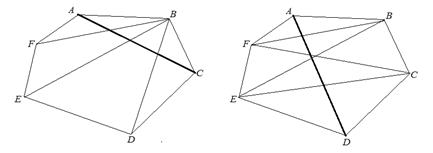
Всего у шестиугольника девять диагоналей и, значит, 9·8 : 2 = 36 пар диагоналей. Осталось понять, сколько пар диагоналей пересекается внутри шестиугольника. Диагонали у шестиугольника бывают двух видов: главные (соединяют противоположные вершины) и неглавные. Например, диагональ AC – неглавная (см. рис.). Всего неглавных диагоналей 6, и каждая пересекает 3 другие диагонали. Главных диагоналей (таких, как AD) всего три штуки, и каждая пересекает четыре другие диагонали. Всего получается (см. рис.) (6·3 + 3·4) : 2 = 15 пар пересекающихся диагоналей.
Ответ
5/12.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь