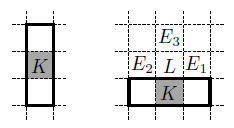
Пусть есть два разных разбиения прямоугольника, у которых совпадают закрашенные клетки. Тогда среди этих закрашенных клеток есть такие, которым в одном разбиении соответствуют вертикальной, а в другом – горизонтальной триминошке (назовем такие закрашенные клетки плохими).

  Среди плохих клеток найдём самую верхнюю (любую, если их несколько). Пусть это клеткаKи в первом разбиенииKпокрыта вертикальной, а во втором – горизонтальной триминошкой (см. рис.). Рассмотрим клеткуL– соседнюю сKсверху. Она принадлежит прямоугольнику, поскольку в первом разбиении она покрыта вертикальной триминошкой. Во втором разбиении этой триминошки нет, так что одна из клетокE₁,E₂,E₃– соседейLсправа, слева и сверху – закрашена: это центр триминошки, покрывающейLво втором разбиении. Но в первом разбиенииLпокрыта не ею, так что найденная нами закрашенная клетка – плохая. ОднакоE₁,E₂иE₃лежат вышеK, что противоречит тому, как мы выборуK.

Всегда.