Часть конструкции, описанной в условии задачи, показана на первом рисунке. Так как стороны исходного треугольника являются касательными к описанной окружности треугольника, образованного точками касания, то задачу удобно переформулировать.

  Рассмотрим треугольникАВСи его описанную окружность. Проведём к ней касательнуюlв точкеА, а из серединыМстороныВСпроведём прямуюа, перпендикулярнуюl(рис. справа).Аналогично определим прямыеbиc. Требуется доказать, что прямыеа, bиспересекаются в одной точке.   Заметим, что  OA || a, так как они обе перпендикулярны к l. Пусть Н – ортоцентр треугольника АВС, E – середина АН. Из того, что  ОМ || AН  и известного соотношения  АН = 2OM  (см. задачу 153528) следует, что OAEM и ОEHM – параллелограммы (их противолежащие стороны равны и параллельны). Значит,  ME ⊥ l,  то есть прямые ME и а совпадают. Из параллелограмма ОEHM получим, что ME содержит точку Р – середину P отрезка ОН.

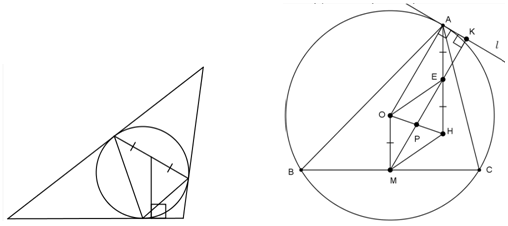
  Проведя аналогичные рассуждения, получим, что прямые b и c также проходят через точку Р. Таким образом, прямые a, b и c пересекаются в одной точке.

Ответ задачи отсутствует