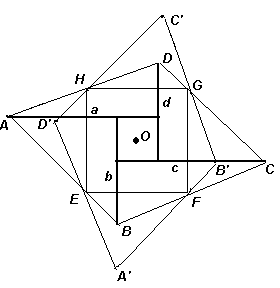
Пусть вершины Е, F, G и Н квадрата ЕFGН лежат на сторонах АВ, ВС, CD и DA параллелограмма АВСD соответственно (см. рис). Перпендикуляры, проведённые из вершин А, В, C и D, обозначены через а, b, c и d соответственно.

  Пусть О – центр квадрата ЕFGН. Достаточно доказать, что повороте с центром О на 90° вершины получившегося четырёхугольника переходят друг в друга.

  Рассмотрим такой поворот, например, против часовой стрелки. КвадратEFGHперейдёт в себя, а образом параллелограммаABCDбудет параллелограммA'B'C'D'. При этом,  A'D'⊥АD  и  C'D'⊥AB  (так как  C'D'⊥CD  и  CD || AB).  Значит, точкаD'– ортоцентр треугольникаАЕН. Следовательно, эта точка лежит на прямойа. Это означает, что при рассматриваемом повороте образом прямойdслужит прямаяа.   Аналогично доказывается, что образами прямыха, bиcявляются прямыеb, cиdсоответственно. Следовательно, точки их попарного пересечения переходят друг в друга, что и требовалось.

Ответ задачи отсутствует