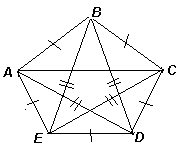
Пусть пятиугольник АВСDE удовлетворяет условию задачи (равны между собой все диагонали, кроме АС, см. рис.). Тогда треугольники АЕD и BCD равны (по трём сторонам), значит,  ∠АЕD = ∠BCD.  Кроме того, треугольник CDE – равнобедренный, поэтому  ∠СЕD = ∠ECD.  Значит,

∠АЕC = ∠BCE.

  Следовательно, равны треугольники АСЕ и ВЕC (по двум сторонам и углу между ними), значит,  АС = ВЕ.  Таким образом, в пятиугольнике равны все диагонали и все стороны, поэтому равны и все углы, то есть пятиугольник – правильный.

Следует.