Задача
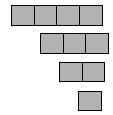
Напомним, что игра в "морской бой" начинается с того, что на доске размером 10×10 клеток расставляют один "корабль" из четырёх клеток, два – из трёх клеток, три – из двух, и четыре одноклеточных (такие, как на рисунке). По правилам "корабли" не должны касаться, даже углами. До какого наименьшего размера можно уменьшить квадратное поле для игры, сохранив это правило?
Решение
Один из возможных примеров расстановки см. на рисунке.

10·1 + 8·2 + 6·3 + 4·4 = 60.
В квадрате размером 6×6 есть только 7·7 = 49 узлов (включая узлы на границе). Следовательно, какие-то узлы должны стать для "кораблей" общими, а это противоречит условию. Второй способ. Разобьём квадрат размером 6×6 на 9 квадратов размером 2×2. В каждом таком квадрате может находиться не более одного "корабля", но всего "кораблей" – 10. Значит, их расставить не удастся (даже, если они все будут одноклеточными!).
Ответ
До квадрата 7×7.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь