Задача
На боковых сторонах AB и BC равнобедренного треугольника ABC отмечены точки E и F соответственно так, что AE = 2BF. На луче EF отмечена точка G так, что GF = EF. Докажите, что угол ACG – прямой.
Решение
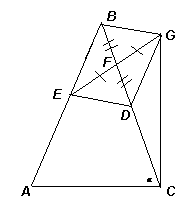
Отметим на стороне ВС точку D так, что BF = FD (см. рис.), тогда в четырёхугольнике BCDE диагонали точкой пересечения делятся пополам, значит, он – параллелограмм. Следовательно, DG = BE.
Кроме того, BD = 2BF = AE, значит, DC = ВС – BD = AB – AE = BE = DG, то есть треугольник CDG – равнобедренный.
Пусть ∠А = ∠С = α, тогда ∠АВС = 180° – 2α. Так как ∠GDВ = ∠В = 180° – 2α и угол GDВ – внешний для треугольника CDG, то
∠DCG = ∠DGC = 90° – α.
Таким образом, ∠ACG = ∠С + ∠DCG = α + 90° – α = 90°.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь