Задача
Высота АН треугольника АВС равна его медиане ВМ. На продолжении стороны АВ за точку В отложена точка D так, что BD = AB. Найдите угол BCD.
Решение
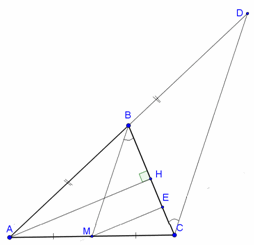
Из точки М опустим перпендикуляр МЕ на сторону ВС. МЕ || АН, значит, МЕ – средняя линия треугольника АНС (см. рис.). Следовательно,
МЕ = ½ АН = ½ BM.
В прямоугольном треугольнике ВМЕ катет МЕ равен половине гипотенузы ВМ, поэтому ∠MBE = 30°. Кроме того, ВМ – средняя линия треугольника ACD, поэтому BM || CD. Значит, ∠BCD = ∠MBC = 30°.
Ответ
30°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет