Задача
На сторонах BC и AC правильного треугольника ABC отмечены точки X и Y соответственно.
Докажите, что из отрезков AX, BY и XY можно составить треугольник.
Решение
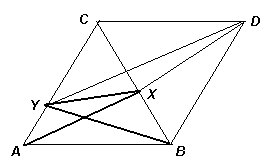
Решение 1: Заметим, что хотя бы один из углов XYA или YXB будет тупым, значит, XY < AX или XY < BX, то есть XY – не наибольший среди трёх данных отрезков (рис. слева).
Если BY ≥ AX, то достроим данный треугольник до ромба ABDC, отразив его относительно стороны ВС. Тогда AX + XY = DX + XY > DY > BY, так как в треугольнике BYD ∠DBY > 60° > ∠BDY.
Если BY < AX, то проводим аналогичное рассуждение, используя симметрию относительно АС.
Таким образом, в любом случае из трёх данных отрезков можно составить треугольник.
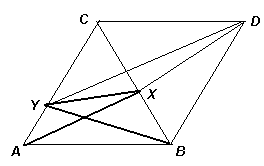
Решение 2: Рассмотрим правильный тетраэдр PABC, основанием которого является данный треугольник (рис. справа). Тогда PX = AX, PY = BY, значит, треугольник PXY – искомый.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь