Задача
В параллелограмме АВСD точка Е – середина стороны AD, точка F – основание перпендикуляра, опущенного из вершины В на прямую СЕ.
Найдите площадь треугольника ABF, если АВ = а, ∠ВАF = α.
Решение
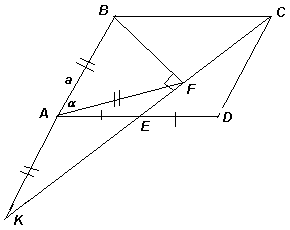
Продлим СЕ до пересечения с прямой АВ в точке K (см. рис.). Из равенства треугольников AKE и DCE следует, что AK = CD = AB. Значит, FA – медиана прямоугольного треугольника KFB, проведённая к гипотенузе, поэтому FA = а. Значит, SABF = ½ AB·AF sin∠ВАF = ½ a² sin α.
Ответ
½ a² sin α.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет