Назад
Задача 165461 • Сложность: 2 • 7-9 класс
Задача

Будем называть клетчатый многоугольник выдающимся, если он не является прямоугольником и из нескольких его копий можно сложить подобный ему многоугольник. Например, уголок из трёх клеток – выдающийся многоугольник (см. рис.).

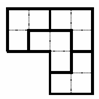
  а) Придумайте выдающийся многоугольник из четырёх клеток.   б) При каких  n> 4  существует выдающийся многоугольник изnклеток?
Решение

  а) Например, уголок из четырёх клеток (см. рис.).

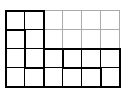
  б) Рассмотрим такой уголок изnклеток, что из двух его копий складывается прямоугольник 2×n. Из таких прямоугольников можно сложить квадрат 2n×2n, а из этих квадратов – уголок, подобный исходному с коэффициентом 2n.
Ответ

При любых.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет