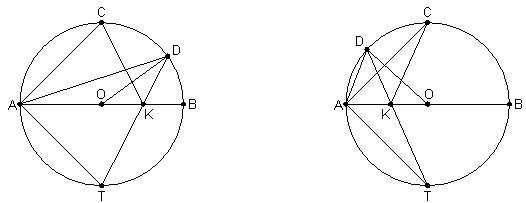
Решение 1:   Пусть прямые AD и BC пересекаются в точке E (см. рис.; случай  D = C  очевиден). Так как  ∠ADK = 45° = ∠EBK,  то точки B, E, D, K лежат на одной окружности. Угол BDE – прямой, значит, и угол BKE – прямой. Следовательно, отрезок AE виден из точек C и K под прямым углом, то есть является диаметром описанной окружности треугольника ACK. Поэтому центр этой окружности лежит на прямой AE, совпадающей с AD.

Решение 2:   Заметим, что точки C и D лежат на окружности с диаметром AB. Если  D = C,  то всё очевидно. Если нет, то угол CDK – прямой, поскольку состоит из двух углов по 45° (см. рис.). Пусть O – вторая точка пересечения прямой AD и описанной окружности треугольника CDK. Тогда угол COK тоже прямой и  ∠OCK = ∠ADK = 45°.  Значит, треугольник COK – прямоугольный и равнобедренный. Так как угол CAK в два раза меньше угла COK и точки A и O лежат по одну сторону от CK, то точка A лежит на окружности с центром O и радиусом  OC = OK.

Решение 3:   Построим окружность на диаметре AB. Точка C делит пополам дугу ADB, биссектриса DK делит пополам другую дугу AB точкой T. Поэтому углы C и T (см. рис.) симметричны относительно AB.

  Так как ещё и углыCAKиTDAопираются на равные дуги, то треугольникиCAKиTDAподобны. ЦентрОописанной окружности треугольникаTDAлежит на луче, отложенном в сторону точкиTот лучаDAна уголADO. Соответственно, центр описанной окружности треугольникаCAKлежит на луче, отложенном в сторону точкиCот лучаAKна такой же угол. Осталось заметить, что углыADOиOAD– равные углы равнобедренного треугольникаAOD.

Ответ задачи отсутствует