Задача
В каждой вершине куба сидело по мухе. Потом все мухи разом взлетели и сели по одной в каждую вершину в каком-то другом порядке.
Докажите, что найдутся три мухи, которые в начальном и конечном положении сидели в вершинах равных треугольников.
Решение
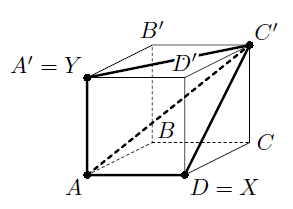
Поскольку куб можно произвольно перевернуть, то можно считать, что муха, сидевшая в вершине A, осталась на месте. Если муха из противоположной вершины C' также осталась на месте, то вместе с любой третьей мухой они образуют нужную тройку. Если же муха из C' переместилась в вершину X, то в C' на её место прилетела третья муха, сидевшая до того в вершине Y. Эти три мухи образуют искомую тройку ввиду равенства треугольников AXC' и AYC' (один из примеров таких треугольников приведён на рисунке).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь