Задача
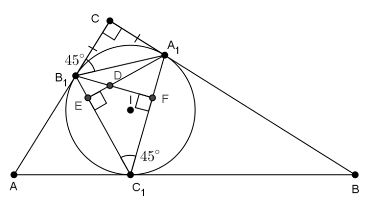
Вписанная окружность прямоугольного треугольника АВС (угол С – прямой) касается сторон АВ, ВС и СА в точках С1, А1, В1 соответственно. Высоты треугольника А1В1С1 пересекаются в точке D. Найдите расстояние между точками C и D, если длины катетов треугольника АВС равны 3 и 4.
Решение
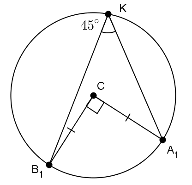
Пусть I – центр вписанной окружности треугольника АВС. Тогда А1IВ1С – квадрат (см. рис.). Заметим, что для треугольника А1В1С1 эта окружность является описанной. Далее можно рассуждать по-разному.

Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет