Задача
На сторонах АВ, ВС и СА равностороннего треугольника АВС выбраны точки D, E и F соответственно так, что DE || АC, DF || BС.
Найдите угол между прямыми AЕ и BF.
Решение
Пусть AЕ и BF пересекаются в точке N. Так как CEDF – параллелограмм, а треугольник BDE – равносторонний, то ВЕ = СF (рис. слева). Далее можно рассуждать по-разному.
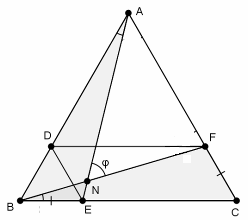
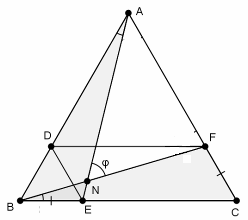
∠ANF = ∠ВАЕ + ∠ABF = ∠CВF + ∠ABF = 60°. Второй способ. Рассмотрим поворот вокруг центра O треугольника АВС на угол 120° против часовой стрелки (рис. справа). При таком повороте вершина А перейдёт в вершину В, сторона ВС – в сторону СА, а так как ВЕ = СF, то точка Е перейдёт в точку F. Следовательно, луч AE перейдёт в луч BF. Угол между этими лучами равен углу поворота, то есть ∠ENF = 120°. Значит, ∠ANF = 60°.
Ответ
60°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь