Задача
Шесть равносторонних треугольников расположены, как на рисунке.
Докажите, что сумма площадей заштрихованных треугольников равна сумме площадей закрашенных треугольников.
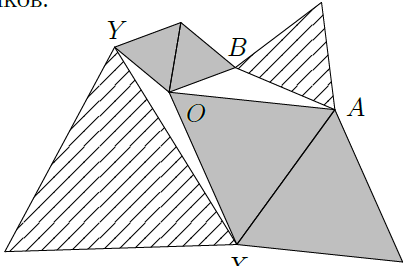
Решение
Обозначим вершины так, как показано на рисунке. Заметим, что OA = OX, OB = OY, а ∠AOB + ∠XOY = 360° – 60° – 120° = 180°, откуда
cos∠XOY = – cos∠AOB. Поскольку площадь равностороннего треугольника со стороной t равна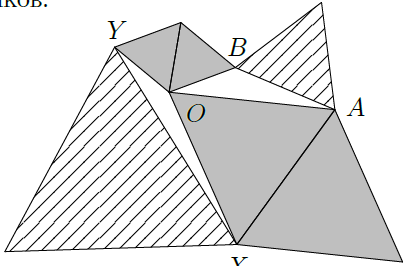 
достаточно доказать, что
AB² + XY² = 2(AO² + BO²). По теореме косинусов для треугольников ABO и XYO имеем AB² = OA² + OB² – 2OA·OB cos∠AOB,
XY² = OX² + OY² – 2OX·OY cos∠XOY. Складывая эти два равенства, получаем требуемое.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет