а) Удвоенная сумма диагоналей четырёхугольника больше его периметра (см. задачу 155152).  Однако  2(1 + 1001) = 2004.   б) Рассмотрим четырёхугольник ABCD, где диагонали перпендикулярны, и диагональ  AC = 1001  делит диагональ  BD = 2  пополам. Его периметр зависит от положения на AC точки пересечения диагоналей K. При движении K от точки A к середине отрезка AC этот периметр непрерывно меняется от 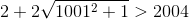    до 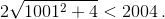    По теореме о промежуточном значении при некотором положении точки K периметр равен 2004.   в) Рассмотрим прямоугольник с диагоналями длины 1001. При изменении угла между диагоналями от 0° до 90° периметр непрерывно изменяется от  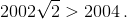   По теореме о промежуточном значении найдётся угол, при котором периметр равен 2004.

а) Не может;  б), в) может.