Задача
На сушке в случайном порядке (как достали из стиральной машины) висит n пар носков. Двух одинаковых пар нет. Носки висят за сохнущей простыней, поэтому Рассеянный Учёный достает по одному носку на ощупь и сравнивает каждый новый носок со всеми предыдущими. Найдите математическое ожидание числа носков, снятых к моменту, когда у Учёного окажется какая-нибудь пара.
Решение
Назовём ξn случайную величину, равную числу снятых носков при условии, что на сушке висит n пар. Очевидно, Eξ1 = 2.
Пусть n > 1. Пронумеруем носки в том порядке, в каком Рассеянный Учёный их снимает с сушки. (Очевидно, способ нумерации не играет роли.) В этой нумерации какой-то носок является последним (его номер 2n, и он никогда не будет снят, поскольку носок с номером n
- 1 наверняка образует пару с каким-либо предыдущим). Отличим как-нибудь этот последний носок: пусть он будет белым.
Обозначим через pj,n вероятность события ξn = j. Очевидно, p1, n = 0.
Найдём p2,n. Все зависит от того, где висит другой белый носок. Если он висит на первом или втором месте (вероятность этого 2/2n–1), то первые два носка пару не образуют. Если же он висит на третьем или последующих местах (вероятность этого равна 2n–3/2n–1), то условная вероятность того, что первые два носка образуют пару равна p2,n–1 – это вероятность получить пару со второй попытки, выбрасывая из последовательности оба белых носка. По формуле полной вероятности
получаем: 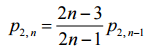 .
.
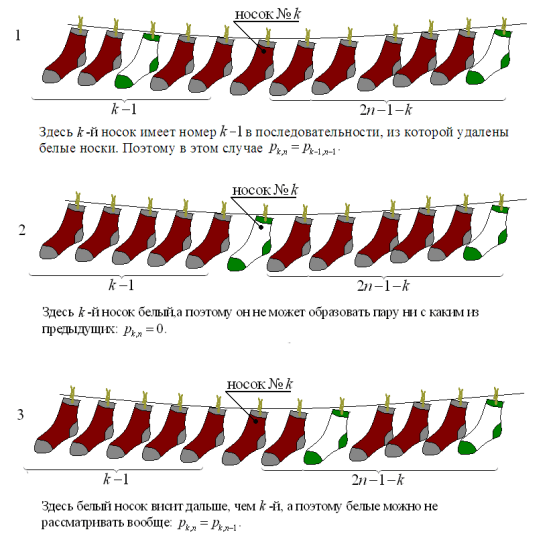
Аналогично найдём p3,n. Если белый носок висит на одном из двух первых мест (с вероятностью 2 /2n–1), то условная вероятность того, что третий носок даст пару, равна вероятности того, что второй носок даст пару в последовательности без белых носков. Если белый носок на третьем месте (вероятность 1/2n–1), то условная вероятность того, что третий носок даст пару, равна 0, поскольку он белый, а парный к нему висит в конце. Если белый носок висит далее третьего места (вероятность 2n–4/2n–1), то условная вероятность того, что первые два носка образуют пару, равна p3,n–1, поскольку в этом случае наличие белых носков роли не играет. Формула полной вероятности даёт: 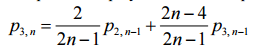 .
.
Рассуждая аналогично и дальше, получаем: 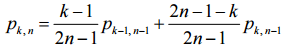 для всех k
от 2 до n.
для всех k
от 2 до n.
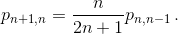 Найдём теперь математическое ожидание:
Найдём теперь математическое ожидание: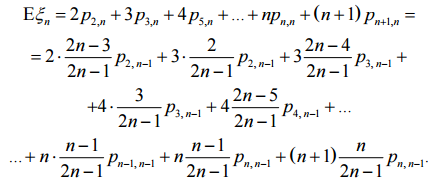
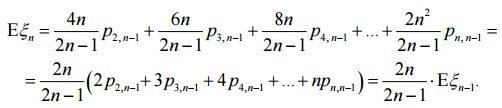
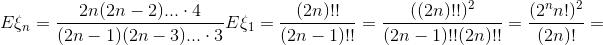
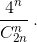
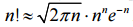 . Получаем:
. Получаем: 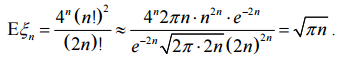
Ответ
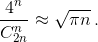
Чтобы оставлять комментарии, войдите или зарегистрируйтесь