Задача
На борту авиалайнера 2n пассажиров, и авиакомпания загрузила для них n порций питания с курицей и n порций с рыбой. Известно, что пассажир с вероятностью 0,5 предпочитает курицу и с вероятностью 0,5 – рыбу. Назовём пассажира недовольным, если ему осталось не то, что он предпочитает.
а) Найдите наиболее вероятное число недовольных пассажиров.
б) Найдите математическое ожидание числа недовольных пассажиров.
в) Найдите дисперсию числа недовольных пассажиров.
Решение
а) Число недовольных пассажиров может быть любым от 0 до n. В случае n = 1 всё очевидно: недовольных либо нет, либо один, причём оба случая равновозможны. Далее считаем, что n > 1.
Введём случайную величину ξ "Число недовольных". ξ = 0, только если ровно n пассажиров предпочитают курицу, а n
остальных – рыбу. Будем считать успехом событие "пассажир хочет курицу . Тогда 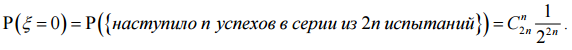
Ровно один пассажир будет недоволен, если число пассажиров, предпочитающих курицу, отличается от n на единицу, то есть число успехов равно
n ± 1. Поэтому P(ξ = 1) = P({n + 1 успех в серии из 2n испытаний}) +
P({n – 1 успех в серии из 2n испытаний}) = 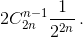
Рассуждая так же, найдём, что 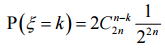 , где k = 1, 2, ..., n.
, где k = 1, 2, ..., n.
В последовательности чисел 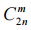 всего 2n + 1 число (это 2n-я строка треугольника Паскаля). Сначала эти числа возрастают при m = 0, 1, ..., n, а потом убывают при m = n, n + 1, ..., 2n. При этом среднее число
всего 2n + 1 число (это 2n-я строка треугольника Паскаля). Сначала эти числа возрастают при m = 0, 1, ..., n, а потом убывают при m = n, n + 1, ..., 2n. При этом среднее число 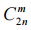 больше других, но меньше, чем удвоенное предыдущее:
больше других, но меньше, чем удвоенное предыдущее: 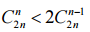 (равенство наступает только при n = 1).
(равенство наступает только при n = 1).
Таким образом, при n > 1 P(ξ = 0) < P(ξ = 1) > P(ξ = 2) > ... > P(ξ = n).
Результат проиллюстрирован на диаграмме распределения случайной величины ξ при n = 5. Для сравнения бледным цветом на том же рисунке дана диаграмма биномиального распределения
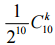 .
.
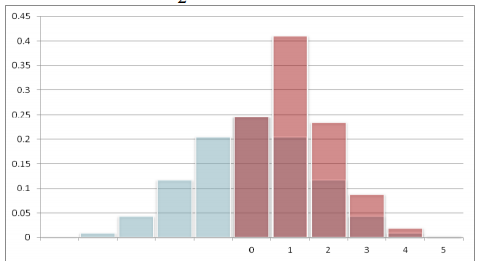
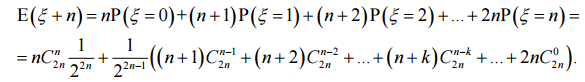
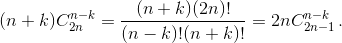 Следовательно, E(ξ +n) =
Следовательно, E(ξ +n) =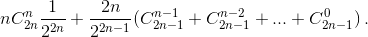 В скобках стоит сумма первой половины всех чисел (2n–1)-й строки треугольника Паскаля. Сумма всех чисел этой строки равна 22n–1, следовательно, сумма в скобках равна 22n–2. Таким образом, E(ξ
+n) =
В скобках стоит сумма первой половины всех чисел (2n–1)-й строки треугольника Паскаля. Сумма всех чисел этой строки равна 22n–1, следовательно, сумма в скобках равна 22n–2. Таким образом, E(ξ
+n) =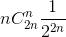 +n, а Eξ = E(ξ +n) –n=
+n, а Eξ = E(ξ +n) –n=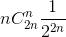 .
Найдём это число приближенно с помощьюформулы Стирлинга
.
Найдём это число приближенно с помощьюформулы Стирлинга 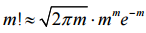 :
: 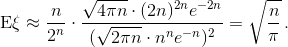 в) Eξ² = 0²·P(ξ = 0) + 1²·P(ξ = 1) + ... + n²P(ξ = n) =
в) Eξ² = 0²·P(ξ = 0) + 1²·P(ξ = 1) + ... + n²P(ξ = n) = 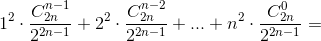
= 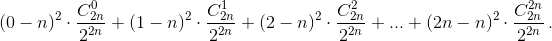
Это выражение в точности равно дисперсии случайной величины η "число успехов в серии из 2n испытаний Бернулли с вероятностью успеха 0,5". Как известно, она равна 2n·0,5·0,5 = n/2.
Следовательно, Dξ = Eξ² – (Eξ)² = 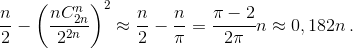
Ответ
а) Если n > 1, то наиболее вероятен один недовольный; если n = 1, то с равными вероятностями либо имеется один недовольный, либо недовольных нет вовсе;
б) 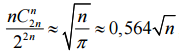 ; в)
; в) 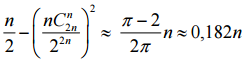 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь