Задача
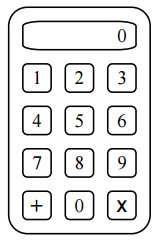
На клавиатуре калькулятора есть цифры от 0 до 9 и знаки двух действий (см. рисунок). Вначале на дисплее написано число 0. Можно нажимать любые клавиши. Калькулятор выполняет действия в последовательности нажатий. Если знак действия нажать подряд несколько раз, то калькулятор запомнит только последнее нажатие. Рассеянный Учёный нажал очень много кнопок в случайной последовательности. Найдите приблизительно вероятность, с которой результат получившейся цепочки действий – нечётное число?
Решение
Будем говорить, что Учёный проделал n шагов, если он набрал n чисел, а между ними n – 1 раз совершил какие-то арифметические действия. Обозначим через pn вероятность того, что после n шагов на калькуляторе будет нечётное число, и выразим pn+1 через pn.
Если последним действием было умножение, то результат будет нечётным, только если оба множителя нечётны; вероятность этого равна ½ pn.
Если последним действием было сложение, то результат будет нечётным, если последнее слагаемое отличается от предпоследнего чётностью; вероятность этого равна ½.
Последнее действие может быть как умножением, так и сложением, и оба этих варианта равновозможны. Поэтому формула полной вероятности даёт:
pn+1 = ½·½ + ½·½ pn = ¼ + ¼ pn.
Переписав это равенство в виде pn+1 – ⅓ = ¼ (pn – ⅓), видим, что при увеличении n на 1 разность pn – ⅓ уменьшается в 4 раза. Следовательно, pn близко к ⅓ при больших n.
Ответ
⅓.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь