Задача
В школьном футбольном турнире участвуют 8 команд, одинаково хорошо играющих в футбол. Каждая игра заканчивается победой одной из команд. Случайно выбираемый по жребию номер определяет положение команды в турнирной таблице:
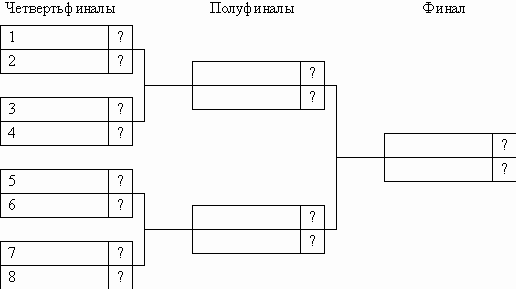
а) встретятся в полуфинале;
б) встретятся в финале.
Решение
а) Для того, чтобы встретиться в полуфинале, команды должны попасть в разные, но сходящиеся к одному полуфиналу подгруппы (событие X).
Команда A может попасть в любую подгруппу. Чтобы команда B могла встретиться с A в полуфинале, она должна попасть в смежную подгруппу.
Вероятность этого 2/7.
Затем и A, и B должны выиграть свои встречи (событие Y). Так как команды одинаково хорошо играют в футбол, то вероятность выигрыша в подгруппе равна ½, и выигрыши команд A и B независимые события, значит, P(Y) = ½·½ = ¼.
Поскольку события X и Y независимы, искомая вероятность равна P(X)P(Y) = 2/7·¼ = 1/14. б) Для того, чтобы встретиться в финале, команде B необходимо попасть в ту половину таблицы, в которую не попала команда A. Соответственно, P(X) = 4/7.
Кроме того, каждой команде необходимо выиграть по два матча. P(Y) = (½)4 = 1/16.
Искомая вероятность равна P(X)P(Y) = 4/7·1/16 = 1/28.
Ответ
а) 1/14; б) 1/28.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь