Пусть P' и Q' – точки, симметричные соответственно точкам P и Q относительно M. Дальше можно рассуждать по-разному.   Первый способ.  QB ⊥ MP'  по условию; кроме того, PBP'C – параллелограмм, так что  P'B || PC ⊥ QM.  Поэтому B – точка пересечения высот треугольника MQP', то есть  P'Q ⊥ MB.  Аналогично  PQ' ⊥ MC.

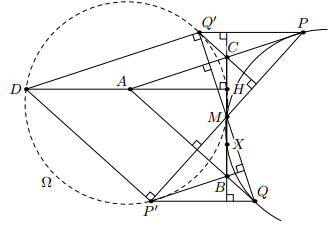
  Построим параллелограмм Q'PAD (см. рис.). Так как Q'PQP' – параллелограмм, то и DAQP' – параллелограмм. Следовательно,  P'D || AQ ⊥ MP',

Q'D || AP ⊥ MQ'  и  DH ⊥ MH. Значит, точки P', Q' и H лежат на окружности Ω с диаметром DM. При симметрии относительно точки M окружность Ω переходит в описанную окружность Ω' треугольника PMQ. При этом точка H, лежащая на Ω, переходит во вторую точку пересечения Ω' и BC, то есть в точку X. Отсюда и следует, что  BH = CX.

  Второй способ. Прямые P'B и Q'C симметричны относительно M прямым PC и QB соответственно. Значит, прямые P'B и Q'C пересекаются в точке A', симметричной A относительно M.

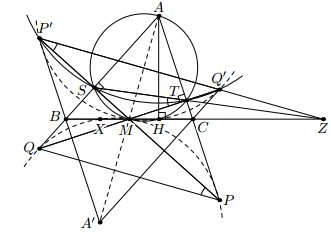
  Пусть прямые P'M и Q'M пересекают соответственно стороны AB и AC в точках S и T. Применим к треугольникам P'SB и Q'TC теорему Дезарга. Точки пересечения пар прямых P'S и Q'T, P'B и Q'C, BS и CT лежат на одной прямой; значит, прямые P'Q', ST и BC пересекаются в одной точке или попарно параллельны. Последний случай невозможен, иначе треугольник ABC был бы равнобедренным.

  ПустьZ– общая точка прямыхP'Q', STиBC. Поскольку  ∠PSQ= ∠PTQ= 90°,  точкиP, Q, S, Tлежат на одной окружности, то есть  ∠QPM= ∠QTS.  Значит,  ∠Q'P'M= ∠QPM= ∠QTS,  то есть и точкиP', Q', S, Tтакже лежат на одной окружности; отсюда  ZP'·ZQ' = ZT·ZS.  С другой стороны, точкиA, M, S, T, Hлежат на окружности с диаметромAM; значит,  ZS·ZT = ZM·ZH.  Следовательно,  ZP'·ZQ' = ZM·ZH,  то есть точкиP', Q', M, Hлежат на одной окружности. Эта окружность симметрична описанной окружности треугольникаPMQотносительно точкиM. Отсюда и следует требуемое.

Ответ задачи отсутствует