Если материки представляют собой вершины правильного тетраэдра, вписанного в сферу, то особых точек ровно четыре – это концы радиусов, проведённых из центра сферы через центры граней тетраэдра.

  Покажем, что пяти и более особых точек не может быть ни при каком расположении четырёх материков. Пусть A – особая точка, r – расстояние от A до ближайших к ней точек суши (не менее трёх из которых по условию лежат на разных материках). Точки океана, удалённые от точки A менее чем на r, образуют сферическую "шапочку" H(A). При этом сферические дуги AX и BY, идущие от разных особых точек A и B к каким-то ближайшим к ним точкам суши X и Y соответственно, могут пересекаться только по концевым точкам, то есть в случае  X = Y.  Действительно, пусть дуги AX и BY пересекаются в точке O и  OY ≤ OX.  Тогда  AY < AO + OY ≤ AO + OX = AX.  Это противоречит тому, что X – ближайшая к A точка суши.

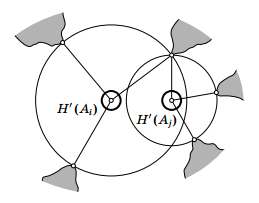
  Пусть есть пять особых точек A₁, ..., A₅. Тогда у каждой из них есть меньшая сферическая "шапочка" H'(A_i), не пересекающаяся ни с какой сферической дугой A_jX, где  j ≠ i  и X – точка суши, ближайшая к A_j (см. рис.). Можно считать, что "шапочки" H'(A_i) попарно не пересекаются и не касаются.

  Добавляя к каждому материку все части дугA_jX, идущие от его точекXдо границ "шапочек"H'(A_j), получим новые материки, которые по-прежнему разделены океаном, для которых точкиA₁, ...,A₅по-прежнему особые (другие особые точки могут исчезнуть) и при этом новые сферические "шапочки"H'(A_j) не пересекаются и не касаются.   Для каждой из точекA₁, ...,A₅зафиксируем тройку материков, доходящих до границы ее новой "шапочки". Каким-то двум из них (скажем,A₁иA₂) соответствует одна и та же тройка материков. Эти материки делят область, ограниченную окружностями "шапочек"H'(A₁) иH'(A₂), на три или более подобластей (если внутри материков есть заполненные океаном "дырки", то таких подобластей может быть сколько угодно), и четвёртый материк целиком лежит в одной из этих подобластей. Назовём эту подобласть Ω.   Все точкиA₃,A₄,A₅лежат в Ω (другие подобласти заполнены океаном и граничат не более чем с двумя материками), и каждой из них соответствует одна и та же тройка материков (четвёртый и те два из первых трёх, которые граничат с Ω). Каждый материк из этой тройки соединяет какие-то две точки на окружностях "шапочек"H'(A₃) иH'(A₄), поэтому океан в разности  Ω \ (H'(A₃) ∪H'(A₄))  разбит на подобласти, каждая из которых граничит не более чем с двумя материками. Ни в одной из этих подобластей точкаA₅лежать не может. Противоречие.

4 особые точки.