При  n = 2  и  n = 3  утверждение задачи проверяется непосредственно (см. рис.).

  Пустьn≥ 4.  Сумма площадейnтреугольников, на которые разрезан единичный квадрат, равна 1, поэтому среди них найдётся треугольник с площадью  S≥¹/_n.  Покажем, что этим треугольником можно накрыть квадрат со стороной¹/_n. Пустьa– наибольшая сторона выбранного треугольника,h– высота, опущенная на эту сторону. Рассмотрим квадрат, одна из сторон которого лежит на сторонеaтреугольника, а еще две вершины находятся на двух других сторонах (см. рис.). Противоположная сторона этого квадрата отсекает треугольник, подобный исходному с коэффициентом подобия  h = ^x/_a = ^h–x/_h,  гдеx– сторона квадрата. Из этого равенства находим  x = ^ah/_a+h.  Если  a + h≤ 2,  то в силу неравенства  S = ^ah/₂≥¹/_n  получаем  x≥²/_n·¹/_a+h≥¹/_n.   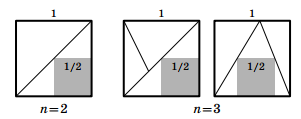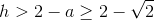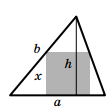Если же  a + h> 2,  то  ,   так как 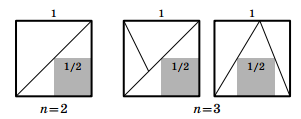   (сторона треугольника не превосходит диагонали исходного квадрата). Кроме того,  a ≥ h.  В самом деле, еслиb– какая-то другая сторона треугольника, то  a ≥ b ≥ h.  Пользуясь этими неравенствами, получаем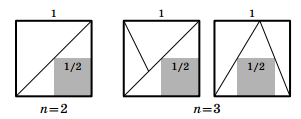  

Ответ задачи отсутствует