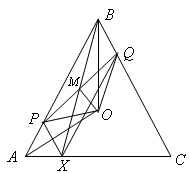
Пусть точка P лежит на стороне AB, а точка Q – на стороне BC.   Первый способ. Поскольку PBQX – параллелограмм,  BP = QX  и  ∠QXC = ∠A = ∠C,  QX = QC = QY.  Значит, точки X, C и Y лежат на окружности с центром Q, поэтому  ∠CYX = ½ ∠CQX = ½ ∠B.  Аналогично  ∠AYX = ½ ∠B.  Отсюда  ∠CYA = ∠B  и, следовательно, точки A, B, C и Y лежат на одной окружности.

  Второй способ.  PX || BQ,  поэтому  ∠A = ∠C = ∠PXA = α. Значит, треугольник APX равнобедренный:  PA = PX = PY.  Следовательно, треугольник APY также равнобедренный, поэтому  ∠YAP = ∠AYP = β.

  Треугольники YPQ и BQP равны из симметрии. Значит, точки B и Y находятся в одной полуплоскости от прямой PQ на одинаковом расстоянии, поэтому  BY || PQ.  Следовательно, BQPY – равнобедренная трапеция, а углы при её основании BY равны:  ∠QBY = ∠PYB = γ.

  Наконец, в четырёхугольнике AYBC  ∠ACB

• ∠AYB = α + β + γ = ∠CAY + ∠CBY,  то есть суммы противоположных углов равны.Таким образом, этот четырёхугольник вписанный.   Третий способ. Пусть O – центр описанной окружности Ω треугольника ABC, M – центр параллелограмма BPXQ. Треугольники AOB и ABC – равнобедренные, поэтому  ∠BAO = ∠ABO = ∠OBQ.  Значит, треугольники APO и BQO равны по двум сторонам и углу между ними. Следовательно,  OP = OQ,  то есть OM – серединный перпендикуляр к PQ.

  Заметим, что точкуYможно получить в два этапа: сначала отразитьXотносительно точкиM, а затем отразить полученную точкуBотносительно прямойOM, перпендикулярнойPQ. Теперь очевидно, чтоYлежит на окружности Ω.

Ответ задачи отсутствует