Задача
Дан неравнобедренный остроугольный треугольник АВС. Вне его построены равнобедренные тупоугольные треугольники АВ1С и ВА1С с одинаковыми углами α при их основаниях АС и ВС. Перпендикуляр, проведённый из вершины С к отрезку А1В1 пересекает серединный перпендикуляр к стороне АВ в точке С1. Найдите угол АС1В.
Решение
Заметим, что ∠АСВ + 2α < 90° + 2·45° = 180°, поэтому отрезок А1В1 пересекает стороны АС и ВС (см. рис.). Пусть точка D симметрична вершине С относительно А1В1, тогда D лежит на отрезке СС1. Кроме того, А1D = А1C = А1B.
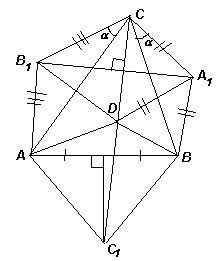
Следовательно, ∠ADC1 = ∠BDC1= 90° – α, то есть DC1 – биссектриса угла АDВ. Точка С1 пересечения биссектрисы треугольника АDВ и серединного перпендикуляра к стороне АВ лежит на описанной окружности этого треугольника. Таким образом, ∠АС1В = 180° – ∠АDВ = 2α.
Ответ
2α.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь